4/22/02 · 数学・算数 不等辺三角形・・・ の面積の表し方を大至急教えて下さい二等辺三角形(にとうへんさんかくけい、英 isosceles triangle )は、三角形の一種で、3 本の辺のうち(少なくとも)2 本の辺の長さが等しい図形である。 長さの等しい 2 辺を等辺といい、残りの 1 辺を底辺とよぶ。2 本の等辺が共有する頂点をとくに二等辺三角形の頂点という。 · 三角形の成立条件について ABCの3辺をa,b,cとすると 三角形の成立条件は、(2辺の長さの和)>(残りの1辺の長さ)なので a+b>c a+c>b b+c>aというのはわかるのですが、 正確には答によると、a+b>cかつa+c>bかつb+c>a とあります。
Newみんなの算数講座8 展開図から見つける高さ 中学受験の算数知恵宝庫
不等辺三角形 辺の長さ 中学
不等辺三角形 辺の長さ 中学-11/29/16 · 辺の長さが2桁でも気にすんな。 三平方の定理(ピタゴラスの定理)の公式にぶち込めばいいんだ。 x² = 5² 12² x = 13 直角三角形と言えども、いつも右下に直角が来るとは限らんぞ。9/7/05 · 三角形において、 「2つの辺の長さa,bが分かっているとき、3つ目の辺の長さxは、 ab


三角形 斜辺 長 さ 直角三角形
今分かっている情報は、 「1辺3角(c=6,A=60°,B=75°,C=45°)」 だよね。 1辺2角を使って他の辺の長さを求めるときには、 正弦定理 を突破口としよう。 aとbどちらから求めにいくのがいいかな? どちらも同じではないんだ。 aに対応する ∠Aは60° 、bに対応する ∠Bは75° だ。 sin60°なら計算できるけれど、sin75°の値は勉強していないよ。 というわけでここは、 ∠A と不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 入力指定 3辺abc 2辺abと高さ (Cは鋭角) 2辺abと高さ (Cは鈍角) 2辺bcと高さ (BとCが鋭角) 2辺bcと高さ (BかCが鈍角) 2辺abと夾角C 辺aと高さと角C 2角BCと夾辺a 2角BCと高さ 面積と2辺ab (Cは鋭角) 面積と2辺ab (Cは鈍角) 面積と2角BC 面積と辺aと角C 面積と高さと角C11/7/18 · 「直角三角形(ちょっかくさんかっけい)」に使う定理なのですが、 上の「3・4・5」センチ(で直角のある)三角形はかなり出てきたりします。 つまり三平方の定理の得には、知らず知らず「不等辺三角形」を相手にすることも多いわけですね。
(3) a, A, b のように1組の辺角(a, A)と他の1つの辺(b)が分かっていれば,角 B が求められる. ※(3)では一般に角度が2つ求まる可能性があるが, A と足すと 180° 以上になる角 B は解にならない.( C が負になって三角形が描けない)3/6/21 · 三角不等式は様々な「長さ」に拡張されています。→いろいろな三角不等式(絶対値,複素数,ベクトル) 三本の不等式を a a a について解くことで,条件を ∣ b − c ∣ < a < b c bc1//13 · 赤い線で示すように、三角形と平行四辺形に分けます。 三角形の三辺の長さは26、65、67となります。 ここでヘロンの公式を使って三角形の面積を出します。 S=√(s・(sa)・(sb)・(sc)) Sは求める面積、a、b、cは辺の長さです。sは下式です。 s=(1/2)×(abc)
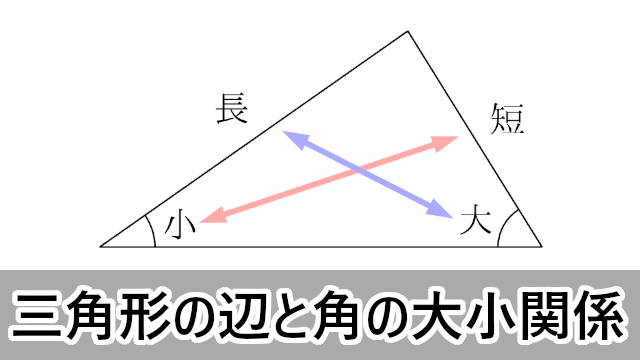
8/12/19 · すべての三角形において、辺の長さとそれに対する角の大きさの大小関係には関係があります。その関係を例も交えつつ紹介し、証明も行いました。 Ⅰ 辺に対する角の大小 Ⅱ 角に対する辺の大小 Ⅰ 辺等脚台形(とうきゃくだいけい、米語: isosceles trapezoid, 英語: isosceles trapezium )は、台形の一種で、1本の底辺の両端の内角が互いに等しい図形である。 このとき、もう一組の底辺の両端の内角も互いに等しくなる。等脚台形は線対称な図形であり、その対称軸は2本の底辺それぞれの中点をデジタル大辞泉 「不等辺三角形」の解説 ふとうへん‐さんかくけい不等辺三角形 どの 辺 の長さも等しくない 三角形 。
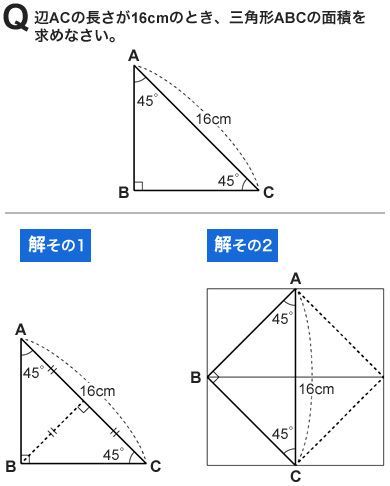


256が解ける子解けない子の差 4つの解法をすぐ思いつくか 2ページ目 President Online プレジデントオンライン


外接円 外心について
余弦定理を変形すれば、 b , c , a が分かっているときに A を求めるという使い方もできます: a 2 =b 2 c 2 −2bc cos A この式をよく見ると、 「右辺は辺の長さだけ」 でできており、 左辺は角度だけ でできています。 したがって、この式を利用すると 「3辺の長さ」から、 「角 A 」 を求める ことができます。 (正確には、角 A そのものではなく cos A が求まりますがStep 1 で, b , A はわかりますが,もう1つの辺の長さ c はわかりません。そこで, c を求めるために,まずC = 180° A B より,C を求めます。 Step 2 Step 1で求めたCを用いて, つまり辺の長さ c を求めます。 これで,2辺 b , c とそのはさむ角 A がわかりました。あとは,公式に当てはめれ三角形の3つの辺がa = 3、b = 4、およびc = 5であるという問題が発生したとします。 三角形の半周長を計算します。 三角形の半周長を見つけるための方程式は次のとおりです。 S = a b c / 2。まず、三角形の3辺すべてを合計します。これは、a b cを意味し



二等辺三角形の底角は本当に等しいのか ひと筋縄ではいかない証明 ブルーバックス編集部 ブルーバックス 講談社 1 4



数学 中3 61 三平方の定理 基本編 Youtube
中学生からの質問(数学) や が出てくるのは,次の2つの特別な直角三角形の場合です。 直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の3/6/21 · 方針: 不等式を三角形の各辺の長さ a, b, c a, b, c a, b, c のみで表してから3変数の不等式を代数的に証明する, というのが幾何不等式証明のもっとも基本的なパターンです。三角形の面積を三辺の長さで表すといえばヘロンの公式が思いつきます。1/11/12 · 6 3辺の長さが3,4、xである三角形abcがある。 7 一辺の長さが1の正三角形abcを底面とする四面体oabcをかんがえる。 8 三角形の中の正方形の辺の長さを求める問題 9 高一の数学です。 「3辺の長さが5√2、17、13である三角形の2番目に大きい角の大きさを求めよ。


三角形 辺 の 長 さ



中学数学 直角三角形の辺の長さの求め方 超丁寧に なぜか分かる はかせちゃんの怪しい研究室
· 中学の三平方の定理教えて下さい 15 x軸方向の角度とy軸方向の角度 16 正三角形の辺の長さを求めるには? 17 不等辺台形面積の計算方法を 18 数学iA 直角三角形の周の長さ 19 正三角形を3つの相似形に分割 もう一問お願いします。二等辺三角形とは?定義・定理・性質や、辺の長さ・角度 直角三角形の辺の長さの求め方と計算ツール 具体例で学ぶ数学 二等辺三角形の性質と辺の長さの求め方!押さえておきたい三 直角三角形の斜辺の長さを求める 3つの方法 wikiHow 二等辺三角形不等辺三角形 不等辺三角形 不等辺三角形の選択した3つの入力値から他の要素の値を計算します。 このページの先頭へ


Newみんなの算数講座8 展開図から見つける高さ 中学受験の算数知恵宝庫



中学数学の図形意味わからん
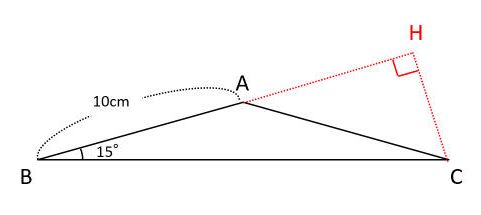
残り2辺の長さを求めることができます。 もちろん \(11\sqrt{2}\)や\(12\sqrt{3}\)という比は覚えておく必要があるからね。 しっかりと覚えておこう! では、特別な直角三角形において 比を使いながら辺の長さを求める練習をしていきましょう。ので中学生でできなくても大丈夫です。 中学校では発展学習として掲載されている教科書があります。 (1) 右図のように 三辺の長さだけ が与えられた三角形で、「 高さAH 」や「 三角形の面積 」を求めるには BH=xとおいて (このときCH=6xとなります) AHの長さ (の2乗)を2とおりの方法で表わせば解けます。 (√13) 2 x 2 = AH 2 = 5 2 (6x) 2 (√13)2x2 = 52 (6x)2 13x 2 =25 (36三角形を作るための条件 三角形には、 2つの辺の長さを足し合わせると残りの1つの辺の長さより長くなる。 また、2の辺の長さを引いた時、残りの1つの辺の長さより短くなる。 という定理がある。この定理の詳細は三角形の2辺の和と差のページを参考にし



頂角36度の二等辺三角形の辺の比を教えてください 頂角36度の二等辺三 数学 教えて Goo


21年 北嶺中学校 算数 2 Vic S粒子
・正三角形(面積から辺と高さ) 正三角形の面積から1辺の長さと高さを計算します。 直角三角形 ・直角三角形(底辺と高さ) 直角三角形の底辺と高さから、斜辺と角度と面積を計算します。9/7/05 · q三角形の、辺の長さ こんにちは、よろしくお願いします。 会社の、施設管理の人から頼まれたんですけど、 現場で材料をカットしたりするのに、 三角形の辺の長さの出し方などを 簡単にまとめた一覧表みたいなものがほしい、 ということなのです。Keisanより h=S/ (a/2)より、 h=a・sin (θ1)・sin (θ2)/sin (θ1θ2) =a・sin (θ1)・sin (θ2)/ (sin (θ1)・cos (θ2)cos (θ1)・sin (θ2)) =a・tan (θ1)・tan (θ2)/ (tan (θ1)tan (θ2)) となり、hの式は合っていると考えられます。 Lの式については、ご指摘ありがとうございます。 Lだけhを使用しているので、後ほど修正(入力パラメータのa,θ1,θ2のみ使用)いたします。


中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋



第12回 平面図形v 三角形 四角形の性質 4年生 日能研の歩き方
三角形と四角形の面積の求め方を覚えましょう。 三角形の面積=底辺×高さ÷2 ※ 「高さ」がどの部分の長さなのかをていねいに考えて下さい。 長方形の面積=たて×よこ 正方形の面積=1辺×1辺 平行四辺形の面積=底辺×高さ ひし形の面積=対角線×対角線÷27/8/16 · 余弦定理を用いた判定法 三角形の $3$ 辺の長さが与えられた時,その三角形が鋭角・直角・鈍角三角形のどれであるかを判定する方法を紹介します.
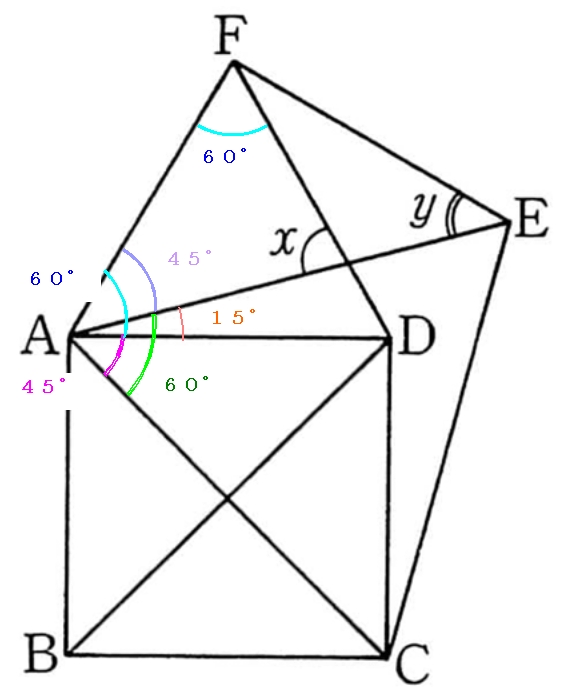


入試に使える算数の基礎 角度の問題



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
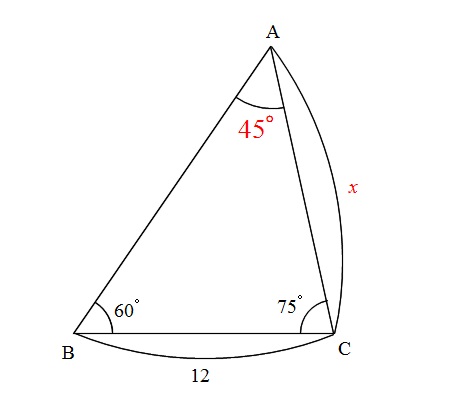


三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない



小学6年生で三角形の面積求め方わかりません 小学6年生の親です 学 数学 教えて Goo



1 の問題で 自分の証明でも合ってますか 字が汚くてすいません Clear


直角三角形 算数解法の極意


誤答から学ぼうシリーズ 余弦定理を用いて三角形を解く ほのぼの数学頑張ろう
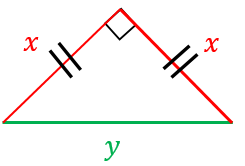


直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
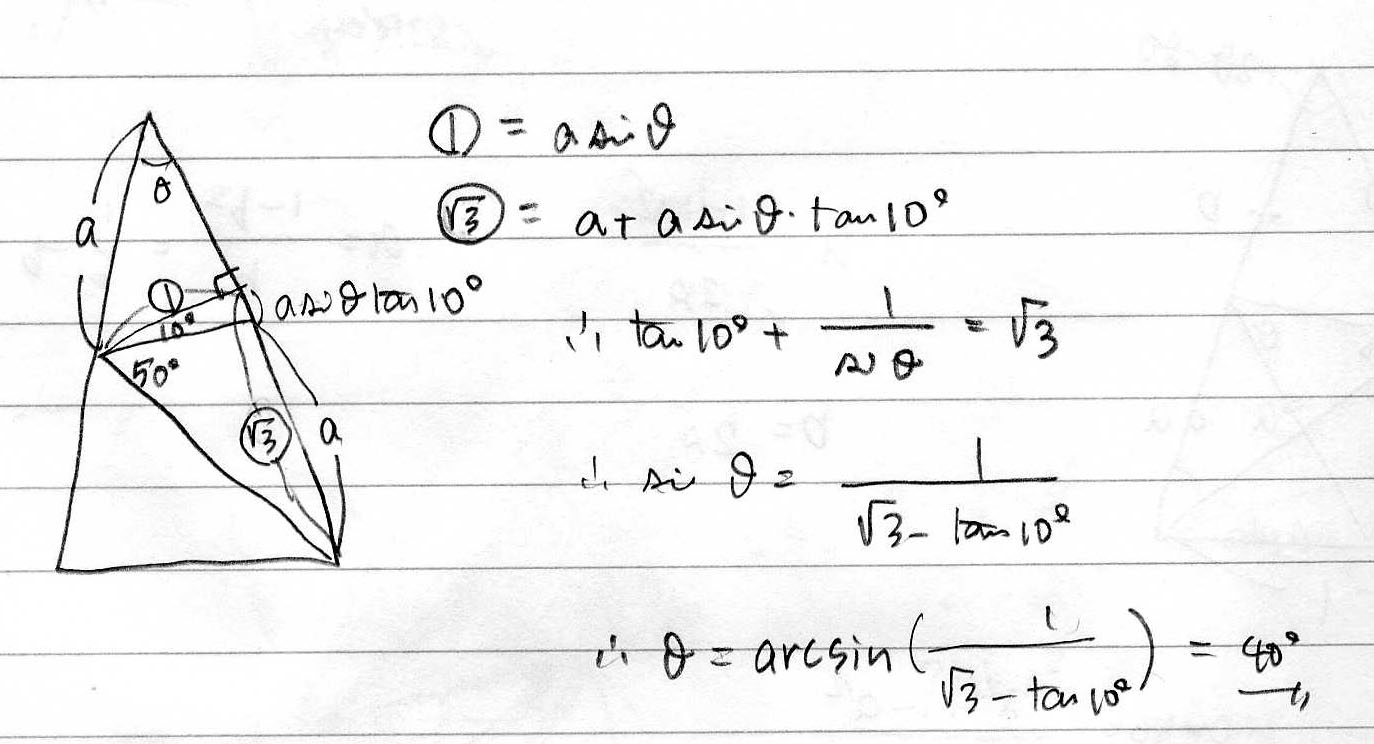


19年08月 東大合格コム



中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン
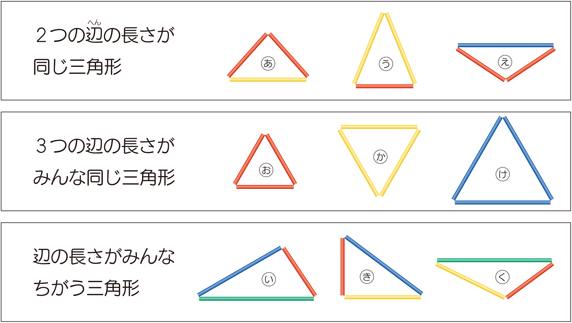


二等辺三角形と正三角形 算数用語集
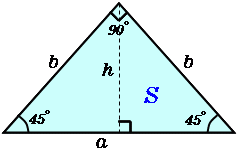


直角二等辺三角形 高精度計算サイト
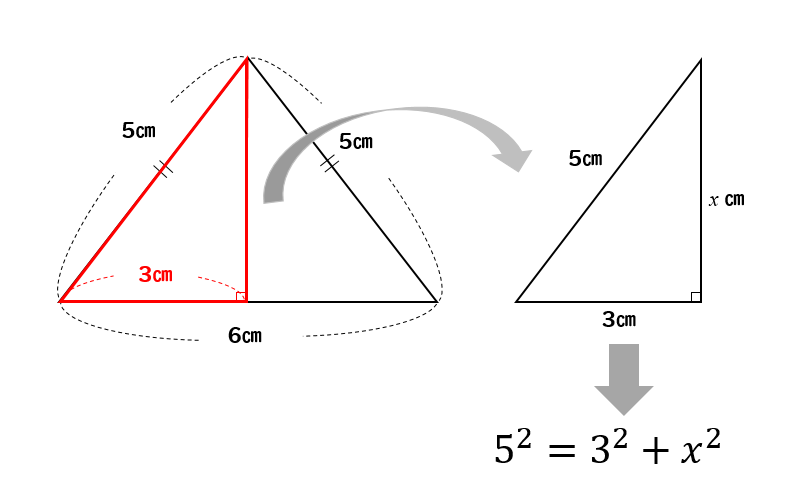


高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ


三角形 二辺 長さ



中学数学 裏技 三角形の角の二等分線の長さを求める下書き やはり俺の考察ブログはまちがっている アニメ 数学



Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集



二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学


三角形の種類 中学から数学だいすき


このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋
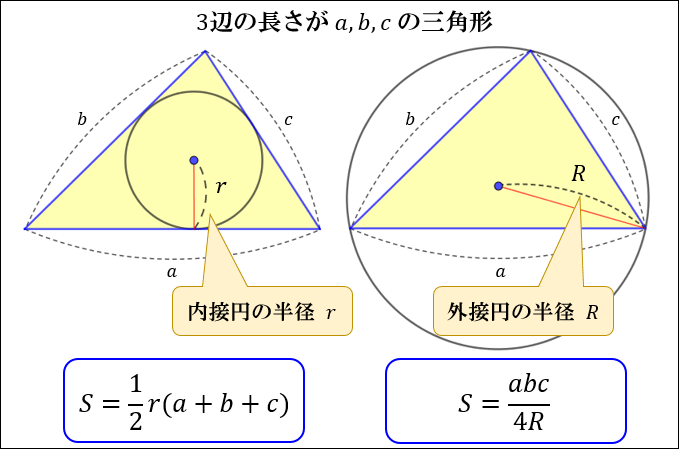


三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



第308回 読むための対話 読むと書くとは大違い 後編 数学ガールの秘密ノート 結城浩 Cakes ケイクス


このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋


誤答から学ぼうシリーズ 余弦定理を用いて三角形を解く ほのぼの数学頑張ろう



小5 算数 小5 42 三角形の面積 Youtube



不等辺三角形 至急ご回答お待ちしております 不等辺三角形について その他 学校 勉強 教えて Goo



二等辺三角形の性質と辺の長さの求め方 押さえておきたい三辺の長さの比
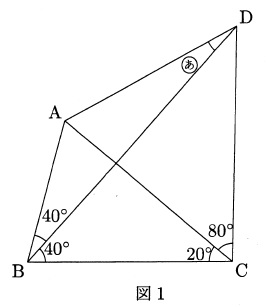


年度 早稲田中学過去問2回目 算数 大問4解説 家庭教師サボの部屋
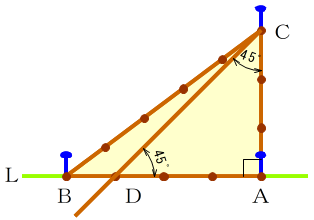


3 4 5の三角形で 本当に直角ができる Note Board



黄金三角形による18 シリーズの三角比 おいしい数学
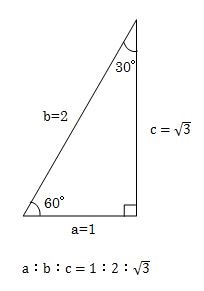


三角比 30 45 60 もう一度やり直しの算数 数学



二等辺三角形の底辺の長さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
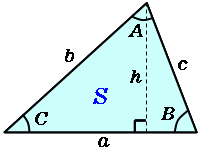


不等辺三角形 高精度計算サイト



中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ



3 4 5の三角形で 本当に直角ができる Note Board



二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学


第18回 え マジっすか そんなの知らなかったテクニック


誤答から学ぼうシリーズ 余弦定理を用いて三角形を解く ほのぼの数学頑張ろう
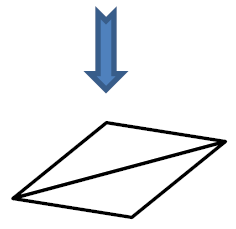


中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン



中学数学 三平方の定理 直角二等辺三角形 オンライン無料塾 ターンナップ



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



三平方の定理の応用


第18回 え マジっすか そんなの知らなかったテクニック



三角形 斜辺 長 さ 直角三角形



三角形 辺 の 長 さ



解答 オリジナル問題2 2つの辺の長さが同じ三角形 図形問題で柔らか頭に 算数オリピック 中学入試問題にチャレンジ
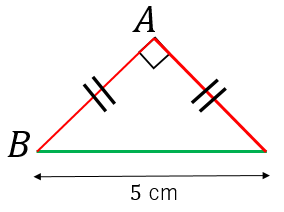


直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学



直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学



二等辺三角形 直角三角形の定義 合同条件と証明問題 リョースケ大学



中学数学 直角三角形の辺の長さの求め方 超丁寧に なぜか分かる はかせちゃんの怪しい研究室



黄金三角形による18 シリーズの三角比 おいしい数学
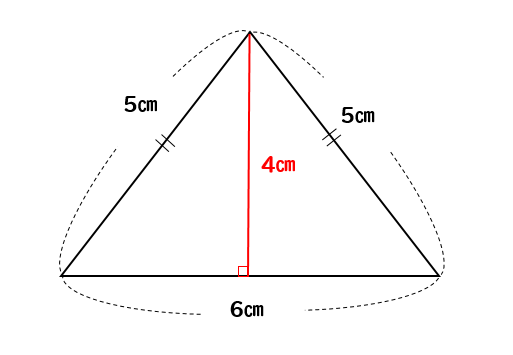


高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ


中2数学 図形の中でも重要なものの1つ 二等辺三角形について徹底解説 まなビタミン



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
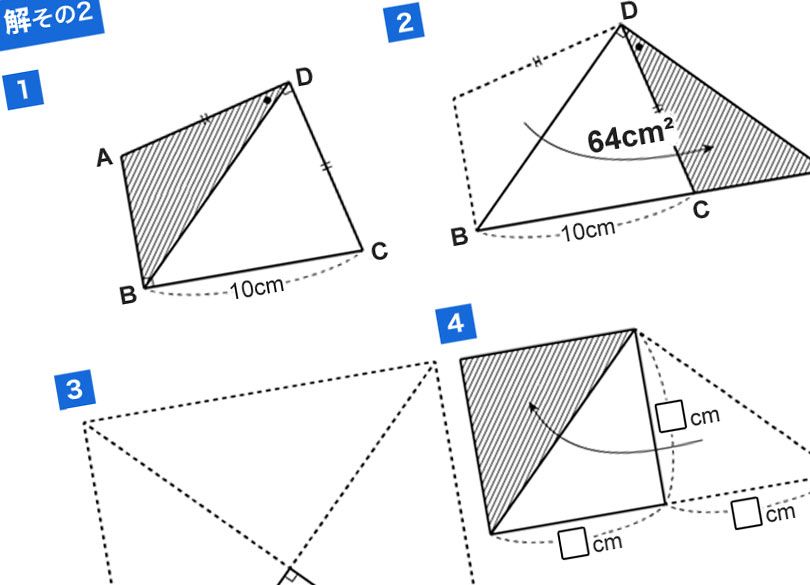


256が解ける子解けない子の差 4つの解法をすぐ思いつくか 2ページ目 President Online プレジデントオンライン


中学から数学だいすき



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ
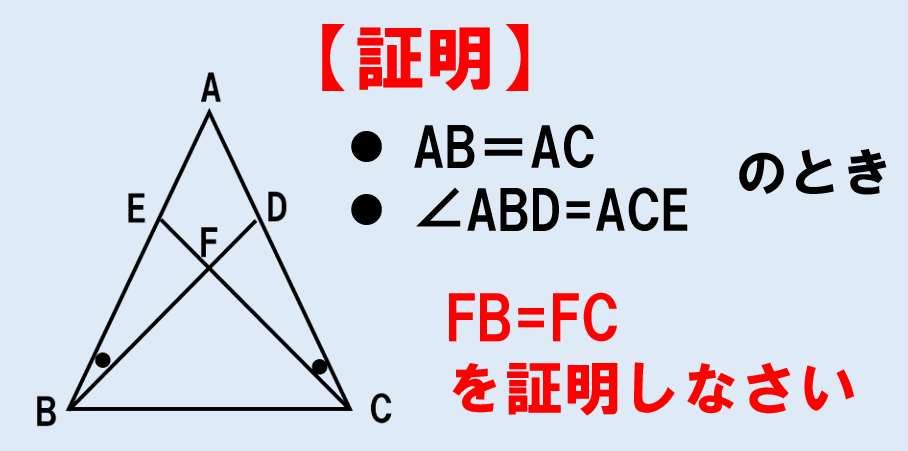


中2数学 2角が等しい三角形 二等辺三角形の長さを用いた証明 授業わかるーの Byナオドット先生 中学数学のわかりやすい解説サイト


三角錐の展開図の作り方 書き方 手順をわかりやすく解説 受験辞典


このように 不等辺三角形の2つの辺の長さと その間の角の Yahoo 知恵袋


辺の長さに注目する 中学受験 田中貴 Com



三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく
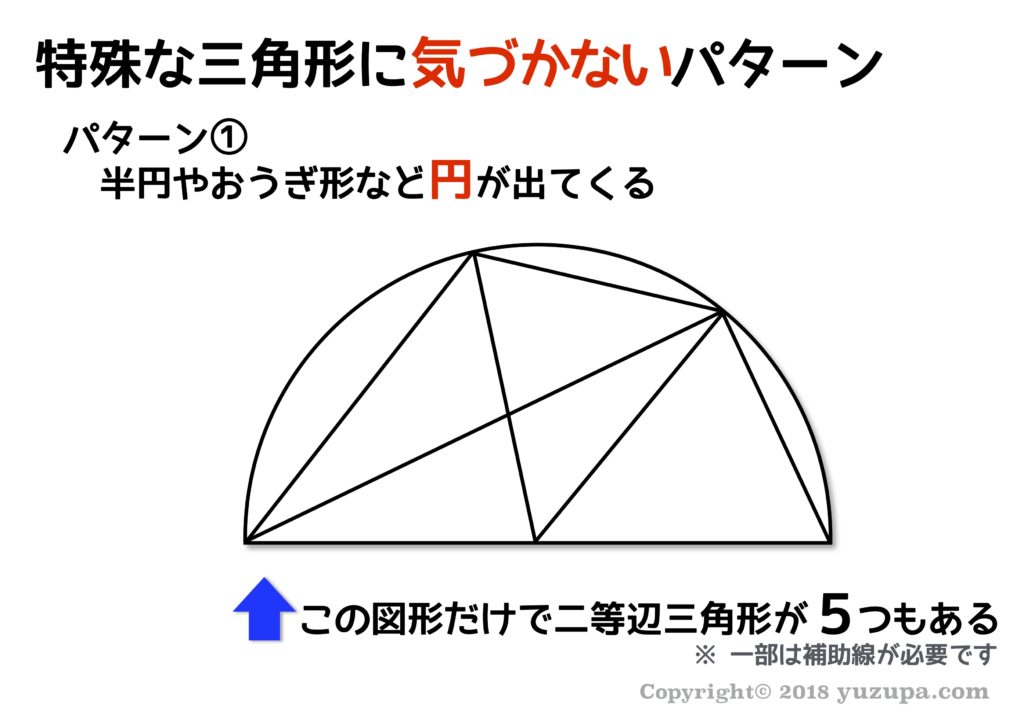


中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋
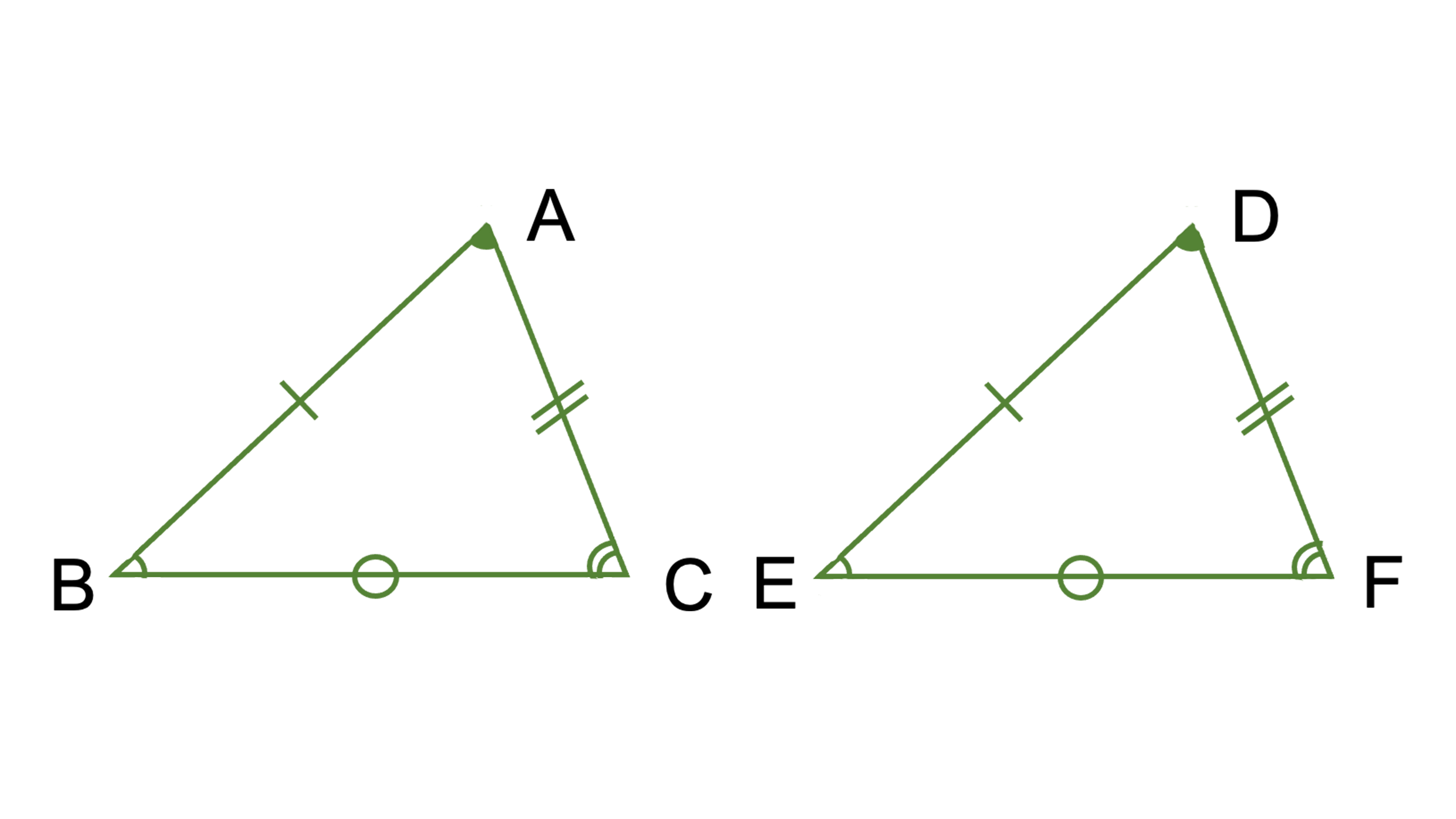


三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



三平方の定理を簡単に理解 更に理解を深めよう 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導



三角比 30 45 60 もう一度やり直しの算数 数学
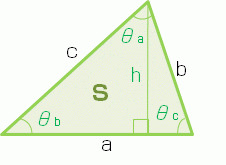


三角形の公式 Wakatta
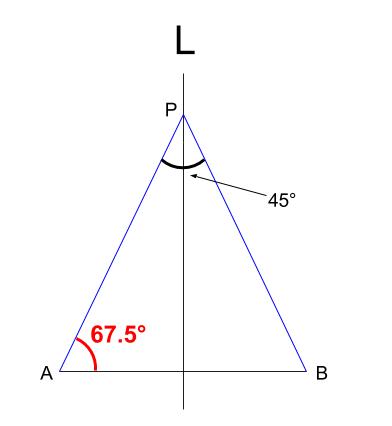


45 の作図 円周角の定理の利用 中学数学の無料オンライン学習サイトchu Su
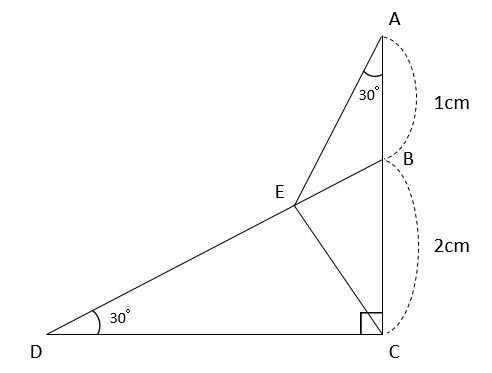


相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室



簡単公式 直角二等辺三角形の辺の長さの2つの求め方 Qikeru 学びを楽しくわかりやすく



二等辺三角形の面積を求める算数の公式は



直角二等辺三角形の辺の長さの求め方 具体例で学ぶ数学
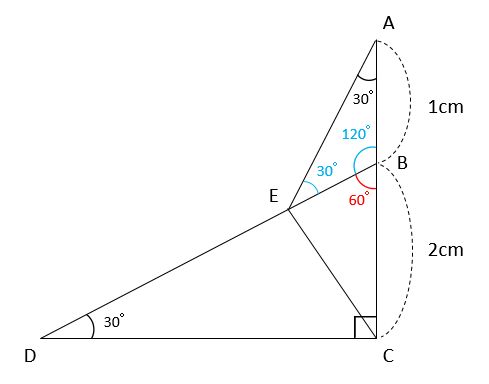


相似比と底辺比から面積比を求める 基準となる三角形を探せ みみずく戦略室


三角形の 合同条件 とは 直角三角形の2つも覚えて証明問題を攻略しよう お役立ち情報ページ 個別指導の学習塾なら個別指導塾スタンダード



二等辺三角形の新着記事 アメーバブログ アメブロ



17 マイヤーズの三角形 まとめ テスターちゃん 4コマ漫画
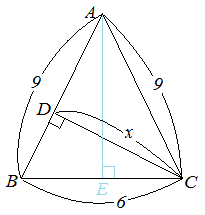


三平方の定理の応用



二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ


辺の長さに注目する 中学受験 田中貴 Com


外接円 外心について



高さがわからない二等辺三角形の面積の求め方 三平方の定理を使えばバッチリ 数スタ



三角形の角の二等分線と辺の比の証明 数学a By となりがトトロ マナペディア



Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
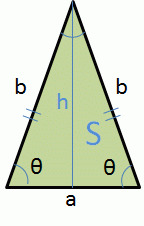


三角形の公式 Wakatta


二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



No comments:
Post a Comment